MULTIPLE REGRESSION

(Note: CCA is a special kind of multiple regression)

 
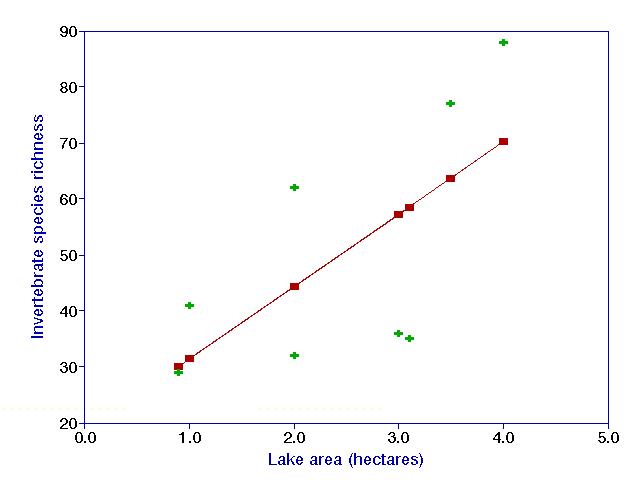
The below represents a simple, bivariate linear regression on a hypothetical data set.  The green crosses are the actual data, and the red squares are the "predicted values" or "y-hats", as estimated by the regression line.  In least-squares regression, the sums of the squared (vertical) distances between the data points and the corresponding predicted values is minimized.

However, we are often interested in testing whether a dependent variable (y) is related to more than one independent variable (e.g. x1, x2, x3).
We could perform regressions based on the following models:
y = ß0 + ß1x1 + e
y = ß0 + ß2x2 + e
y = ß0 + ß3x3 + e
And indeed, this is commonly done. However it is possible that the independent variables could obscure each other's effects. For example, an animal's mass could be a function of both age and diet. The age effect might override the diet effect, leading to a regression for diet which would not appear very interesting.

One possible solution is to perform a regression with one independent variable, and then test whether a second independent variable is related to the residuals from this regression. You continue with a third variable, etc. A problem with this is that you are putting some variables in privileged positions.

A multiple regression allows the simultaneous testing and modeling of multiple independent variables. (Note: multiple regression is still not considered a "multivariate" test because there is only one dependent variable).

The model for a multiple regression takes the form:
y = ß0 + ß1x1 + ß2x2 + ß3x3 + ..... + e 

And we wish to estimate the ß0, ß1, ß2, etc. by obtaining
^
y1 = b0 + b1x1 + b2x2 + b3x3 + .....

The b's are termed the "regression coefficients".  Instead of fitting a line to data, we are now fitting a plane (for 2 independent variables), a space (for 3 independent variables), etc.

The estimation can still be done according the principles of linear least squares.
The formulae for the solution (i.e. finding all the b's) are UGLY. However, the matrix solution is elegant:

The model is: Y = Xß + e
The solution is: b =(X'X)-1X'Y

(See for example, Draper and Smith 1981)

As with simple regression, the y-intercept disappears if all variables are standardized (see Statistics) .


LINEAR COMBINATIONS

Consider the model:
y = ß0 + ß1x1 + ß2x2 + ß3x3 + ..... + e 
Since y is a combination of linear functions, it is termed a linear combination of the x's.   The following models are not linear combinations of the x's:
y = ß0 + ß1/x1 + ß2x22 + e 
y = exp(ß0 + ß1x1 + ß2x2 + ß3x3 + e)

But you can still use multiple regression if you transform variables. For the first example, create two new variables:
x1' = 1/x1 and x2' = x22

For the second example, take the logarithm of both sides:
log(y) = ß0 + ß1x1+ ß2x2 + ß3x3 + e

There are some models which cannot be "linearizable", and hence linear regression cannot be used, e.g.:
y = (ß0 - ß1x1)/3x2 + e

Or, subtly,
y = exp(ß0 + ß1x1 + ß2x2 + ß3x3) + e

These must be solved with nonlinear regression techniques. Unfortunately, it is hard to find the solution to such nonlinear equations if there are many parameters.


What about polynomials?

Note that:
y = ax3 + bx2 + cx + d + e 

can be expressed as:
y = ß0 + ß1x1+ ß2x2 + ß3x3 + e 

if x1 = x1, x2 = x2, x3 = x3

So polynomial regression is considered a special case of linear regression. This is handy, because even if polynomials do not represent the true model, they take a variety of forms, and may be close enough for a variety of purposes.
 

If you have two variables, it is possible to use polynomial terms and interaction terms to fit a response surface:
y = ß0 + ß1x1+ ß2x12 + ß3x2 + ß4x22 + ß4x1x2 + e 

This function can fit simple ridges, peaks, valleys, pits, slopes, and saddles.   We could add cubic or higher terms if we wish to fit a more complicated surface.

ß4x1x2 is considered an interaction term, since variables 1 and variable 2 interact with each other.  If b4 ends up being significantly different from zero, then we can reject the null hypothesis that there is 'no interaction effect'.


Statistical inference
Along with a multiple regression comes an overall test of significance, and a "multiple R2" - which is actually the value of r2 for the measured y's vs. the predicted y's.  Most packages provide an "Adjusted multiple R2" which will be discussed later.
For each variable, the following is usually provided:

The standardized coefficient is handy: it equals the value of r between the variable of interest and the residuals from the regression, if the variable were omitted.

The significance tests are conditional: This means given all the other variables are in the model. The null hypothesis is: "This independent variable does not explain any of the variation in y, beyond the variation explained by the other variables".  Therefore, an independent variable which is quite redundant with other independent variables is not likely to be significant.

Sometimes, an ANOVA table is included.

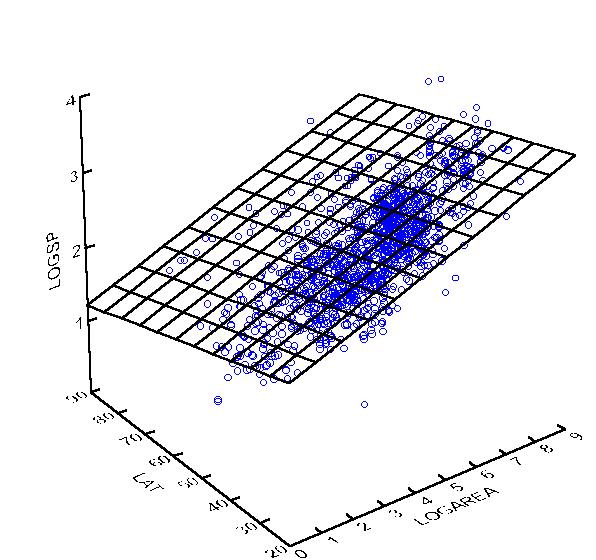
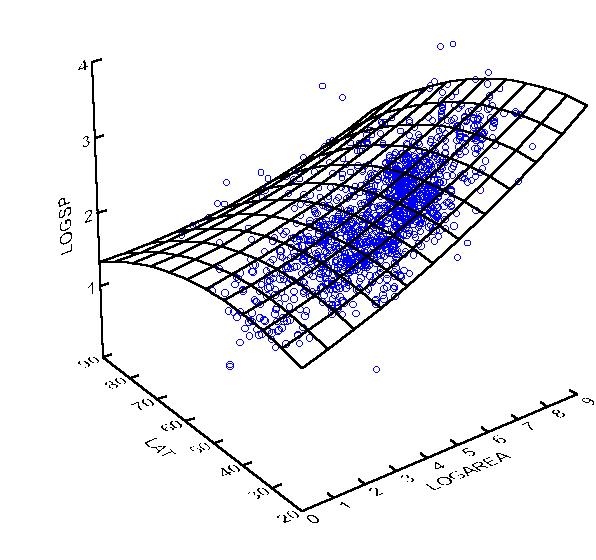
The following is an example SYSTAT output of a multiple regression: 

Dep Var: LOGSP   N: 1412   Multiple R: 0.7565   Squared multiple R: 0.5723
 
Adjusted squared multiple R: 0.5717   Standard error of estimate: 0.2794
 
Effect         Coefficient    Std Error     Std Coef Tolerance     t   P(2 Tail)
 
CONSTANT            2.4442       0.0345       0.0        .      70.8829   0.0000
LOGAREA             0.1691       0.0040       0.7652    0.9496  42.7987   0.0000
LAT                -0.0136       0.0008      -0.2993    0.9496 -16.7381   0.0000
 
                             Analysis of Variance
 
Source             Sum-of-Squares   DF  Mean-Square     F-Ratio       P
 
Regression              147.1326     2      73.5663    942.6110      0.0000
Residual                109.9657  1409       0.0780


It is possible for some variables to be significant with simple regression, but not with multiple regression. For example:

Plant species richness is often correlated with soil pH, and it is often strongly correlated with soil calcium. But since soil pH and soil calcium are strongly related to each other, neither explains significantly more variation than the other.

This is called the problem of multicollinearity (though whether it is a 'problem', or something that yields new insight, is a matter of perspective).

It is also possible that nonsignificant patterns in simple regression become significant in multiple regression, e.g. the effect of age and diet on animal size.


Problems with multiple regression
 

Overfitting:

The more variables you have, the higher the amount of variance you can explain. Even if each variable doesn't explain much, adding a large number of variables can result in very high values of R2. This is why some packages provide "Adjusted R2," which allows you to compare regressions with different numbers of variables.
The same holds true for polynomial regression. If you have N data points, then you can fit the points exactly with a polynomial of degree N-1.
The degrees of freedom in a multiple regression equals N-k-1, where k is the number of variables. The more variables you add, the more you erode your ability to test the model (e.g. your statistical power goes down).
 

Multiple comparisons:

Another problem is that of multiple comparisons. The more tests you make, the higher the likelihood of falsely rejecting the null hypothesis.

Suppose you set a cutoff of p=0.05.  If H0 is always true, then you would reject it 5% of the time.   But if you had two independent tests, you would falsely reject at least one H0 
1-(1-.05)2 = 0.0975, or almost 10% of the time.

If you had 20 independent tests, you would falsely reject at least one H0
1-(1-.05)20 = 0.6415, or almost 2/3 of the time.

There are ways to adjust for the problem of multiple comparison, the most famous being the Bonferroni test and the Scheffe test. But the Bonferroni test is very conservative, and the Scheffe test is often difficult to implement.
For the Bonferroni test, you simply multiply each observed p-value by the number of tests you perform.

Holm's method for correcting for multiple comparisons is less well-known, and is also less conservative (see Legendre and Legendre, p. 18).


Partial Correlation
Sometimes you have one or more independent variables which are not of interest, but you have to account for them when doing further analyses. Such variables are called "covariables", and an analysis which factors out their effects is called a "partial analysis". Examples include:

(For the simplest case, a partial correlation between two variables, A and B, with one covariable C, is a correlation between the residuals of the regression of A on C and B on C. The only difference is in accounting for degrees of freedom).

Examples: Suppose you perform an experiment in which tadpoles are raised at different temperatures, and you wish to study adult frog size. You might want to "factor out" the effects of tadpole mass.

In the invertebrate species richness example, Species Richness is related to area, but everyone knows that. If we are interested in fertilization effects, it might be justifiable to "cancel out" the effects of lake area.


Stepwise Regression

Often, you don't really care about statistical inference, but would really like a regression model that fits the data well. However, a model such as:

y = ß0 + ß1x1 + ß2x2 + ß3x3 + ß4x4 + ß5x5 + ß6x6 + ß7x7 + ß8x8 + ß9x9 + ß10x10 + ß11x11 + ß12x12 + ß13x13 + ß14x14 + ß14x14 + e

Is far too ungainly to use! It might be much more useful to choose a subset of the independent variables which "best" explains the dependent variable.

There are three basic approaches:

1) Forward Selection

Start by choosing the independent variable which explains the most variation in the dependent variable.
Choose a second variable which explains the most residual variation, and then recalculate regression coefficients.
Continue until no variables "significantly" explain residual variation.

2) Backward Selection

Start with all the variables in the model, and drop the least "significant", one at a time, until you are left with only "significant" variables.

3) Mixture of the two

Perform a forward selection, but drop variables which become no longer "significant" after introduction of new variables.
 

In all of th above, why is "significant" in quotes? Because you are performing so many different comparisons, that the p-values are compromised.  In effect, at each step of the procedure, you are comparing many different variables.  But the situation is actually even worse than this: you are selecting one model out of all conceivable sequences of variables.

Although stepwise methods can find meaningful patterns in data, it  is also notorious for finding false patterns.  If you doubt this, then try running a stepwise procedure using only random numbers.  If you include enough variables, you will almost invariably find 'significant' results.


This page was created and is maintained by Michael Palmer.
 To the ordination web page